<루파>(Route Finding)하고 문제해결을 시작하라.
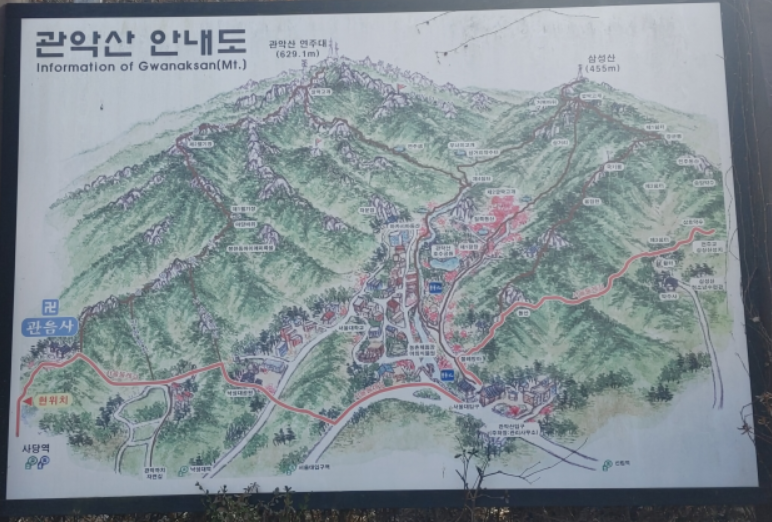
<루트 파인딩>은 등반에서만 중요한 것이 아니라, 수학문제의 해결에서도 매우 중요합니다. 우리가 서울에 있는 <관악산>을 간다고 가정해보겠습니다. 몇 번 가본 사람의 경우도 마찬가지이지만, 특히 처음 가본 사람은 산행을 시작하는 곳에서 다음과 같은 <안내도>를 보고 어떻게 오르고 내려갈 것인지를 생각하는 것은 <필수>라고 할 수 있습니다.

그런데 가장 중요하다고 할 수 있는 수학시험을 볼 때에는 <어떤 과정을 거쳐서 문제를 해결할 것인가>를 전혀 생각하지 않고, 기계적으로 문제를 해결하는 경우가 많습니다. 이런 경우는 <이미 여러번 경험해본 문제>가 아니면 언제든 <예상하지 못한 변수>가 발생하고, 이로 인하여
(1) 문제를 해결하는 시간이 생각보다 오래 걸리거나
(2) 문제를 해결하는 과정에서 <실수>라고 하는 <습관적인 잘못>을 하여 문제를 틀리거나
(3) 예상하지 못한 상황에 당황하여 그 문제뿐 아니라 시험 전체를 망치는 일을 겪게 됩니다.
< 2024.9월 모의고사 > 미적분 소재의 문항으로 Route Finding 하는 <훈련>을 해보도록 하겠습니다. 훈련할 문항은 다음과 같습니다.
※ 다음의 빈 칸에 필요한 내용을 채워보기를 바랍니다.

6번 문제를 소재로 예시를 들어보겠습니다. 
이 문제를 해결하는 <대표적인 방법>은 세 가지 정도가 있습니다.

(1) 세 가지 방법 모두 문제의 답을 <문제해결에 필요한 시간내에> 구할 수 있습니다.
(2) 그럼에도 불구하고 세 가지 방법의 차이는 있으며 가능하면 효과적인 방법으로 해결하면 좋습니다.
(3) 이때 효과적인 방법은 <생각하는 시간>+<계산하는 시간>을 고려해서 판단해야 합니다.
문제해결의 이러한 특징을 고려하면, 문제를 해결하는 것을 <시작하기 전>에 <루파>(Route Finding)는 것은 매우 중요하다고 할 수 있습니다. 자, 그렇다면 세 가지 방법의 경우 <시작하기 전>에 어떻게 <루파>를 할 수 있을지 생각해보기 바랍니다. 그리고 다음의 문제들에 스스로 생각한 것을 적용하여 한번 <훈련>해보기를 권합니다.
이 과정에서 다음의 결론을 내릴 수 있다면 <한 단계의 발전>을 이룰 수 있을 것입니다.
(1) <기계적으로> 문제를 해결하는 것과 비교할 때 <루파>하고 해결하면 계산을 효과적으로 할 수 있다.
(2) <루파>하고 문제를 해결하면, 설령 가장 효율적인 루트를 찾지 못해도 예측한 과정으로 문제를 <시험시간내>에 해결하는 것이 충분히 가능하다.
(3) 2024학년도 9월 모의평가의 문제들은 다음의 원칙에 따라서 출제되었음이 분명하다.

[출처-수놀음]
원본
https://cafe.naver.com/sunoleum/1072
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.






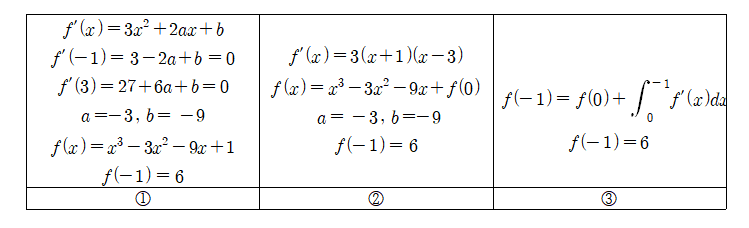






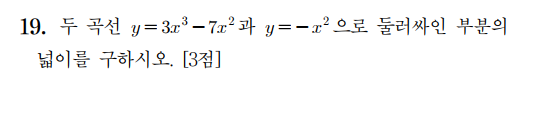
















첫번째 댓글의 주인공이 되어보세요.