난만한님의 벡터문제 No.2 변형문제에요+_+
게시글 주소: https://video.orbi.kr/0003141948
http://orbi.kr/bbs/board.php?bo_table=united&wr_id=1650014&sca=&sfl=wr_subject&stx=%EC%9D%B4%ED%95%B4%EC%9B%90&page=2
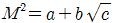라 한다. a+b+c는? (단, 점 A,C,G,T는 한 평면 위에 있고, c는 1이 아닌 어떤 수의 제곱으로 나누어떨어지지 않는다.) [4점]
이 문제 변형입니다.
한 변의 길이가 루트3인 정사면체 ABCD가 있다. 삼각형 ACD의 무게중심을 G라 하고, 평면 ABC, ABD, ACD, BCD와 접하는 구 중 삼각형 BCD 내에 접점이 있고 정사면체 내부에 존재하지 않는 구를 구 O1이라 하자.
구 O2는 구 O1과 점 T에서 외접하고, 두 구의 공통 접평면 중 평면 BCD와 평행한 평면이 존재하는 구들 중 큰 구이다.
점 P가 구 O2 위의 임의의 점이라 할 때,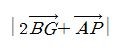 
의 최댓값을 M이라 하자. 이 때 정수 c와 유리수 a,b에 대해
의 최댓값을 M이라 하자. 이 때 정수 c와 유리수 a,b에 대해라 한다. a+b+c는? (단, 점 A,C,G,T는 한 평면 위에 있고, c는 1이 아닌 어떤 수의 제곱으로 나누어떨어지지 않는다.) [4점]+) 같은 평면끼리도 서로 평행하다고 생각합니다.
포만한 수리 연구소, 수능콕콕 바늘공부방에도 올렸어요. 여기에도 올려봐요~
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
첫번째 댓글의 주인공이 되어보세요.